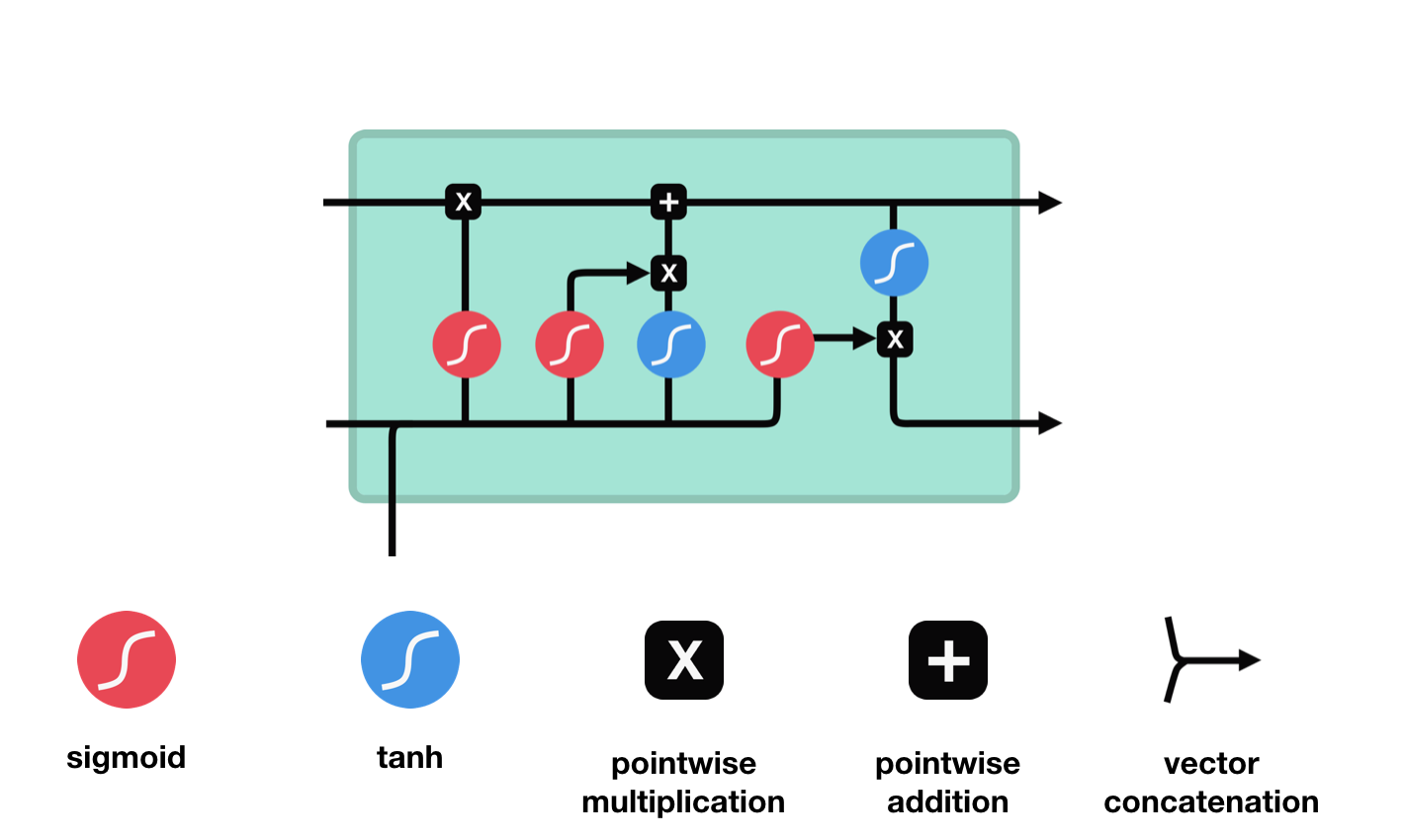
Long Short-Term Memory (LSTM)
Besides output, a cell also has "memory".
Formula
Memory: $$ \begin{aligned} c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \\ &= (\text{Forget Old Info}) + (\text{Incorporate New Info}) \\ &= \boxed{\text{Lont-Term Memory}} + \boxed{\text{Short-Term Meomry}} \end{aligned} $$ where: $$ \begin{aligned} x_{t} &= \begin{bmatrix}w_{t} & h_{t-1} \end{bmatrix} &[\text{synthesized input}] \\ \tilde{c}_n &= \tanh(\mathbf{W_c} \cdot x_{t} + b_c) &[\text{new experience}]\\ f_t &= \sigma(\mathbf{W_f} \cdot x_{t} + b_f) &[\text{forget control}] \\ i_t &= \sigma(\mathbf{W_i} \cdot x_{t} + b_i) &[\text{input control}] \\ \end{aligned} $$ Output: $$ \begin{aligned} o_t &= \sigma(\mathbf{W_o} \cdot x_{t} + b_o) &[\text{output control}] \\ h_t &= o_t \odot \tanh(c_t) &[\text{hidden vector = output}] \end{aligned} $$
Gates
- forget gate
- input gate
- output gate
Graph